Chapitres
- 01. Qu'est-ce qu'un tableau de variation d'une fonction ?
- 02. Dériver une somme de fonctions avec constante
- 03. Dériver une fonction avec un produit
- 04. Factoriser si possible la dérivée de f
- 05. Etudier le signe de f'(x) sur l’intervalle I
- 06. Dresser le tableau de variation de f sur I
- 07. Tracer la fonction sur son intervalle de définition
- 08. Dresser un tableau de variation à partir d'une courbe
- 09. Exercice pratique de variation d'une fonction
"Les maths peuvent être définies comme la science dans laquelle on ne sait jamais de quoi l'on parle, ni si ce que l'on dit est vrai." Bertrand Russel (1872-1970).
En classe de Terminale, le problème de l'étude de fonctions est posé tous les ans dans l'épreuve de maths du baccalauréat, et demeure parfois une des bêtes noires des élèves.
En juin 2019
candidats ont obtenu le baccalauréat, avec un taux de réussite moyen de 91,2 % dans les séries générales.
Pour les autres séries technologiques et professionnelles, le taux de réussite a respectivement atteint 88,1 % et 82,3 %.
Voici tout d'abord un exemple de tableau de variation :
| x | f(x) | Variation de f(x) |
|---|---|---|
| -2 | 4 | décroissante |
| -1 | 1 | décroissante |
| 0 | 0 | croissante |
| 1 | 1 | croissante |
| 2 | 4 | croissante |
Dans cet article, la rédaction présente la méthode générale pour étudier les variations d'une fonction f définie sur un intervalle I, dresser son tableau de variations et ensuite, faire sa représentation graphique.

Qu'est-ce qu'un tableau de variation d'une fonction ?
Si ces exercices de mathématiques paraissent parfois simples, une petite erreur de signe peut vite s'immiscer et fausser tout le résultat.

Cela se vérifie souvent pour l'étude des fonctions.
Une fonction affine sous la forme f(x) = ax + b semble simple de prime abord.
Pourtant, on trouve régulièrement des erreurs liées aux changements de signes éventuels.
Si, dans le programme de seconde générale, on étudie comment résoudre une équation de second degré, on considère que les bases du calcul algébrique sont maîtrisées car elles ont été acquises lors de la préparation du brevet des collèges.
En classe de 2nde et en première, les élèves sont déjà initiés à l'étude de fonctions. Pourtant, tous les ans, au baccalauréat, des coquilles s'invitent dans les copies.
Il n'est donc pas inutile de rappeler comment dresser le tableau de variation d'une fonction.
Pour étudier les variations d'une fonction, on étudie une fonction affine, linéaire, polynôme, exponentielle, logarithme ou trigonométrique.
L'étude de fonction à partir de son équation - fonction affine, fonction linéaire, fonction asymptotique, fonction logarithme, fonction exponentielle - consiste à déterminer son sens de variation et ses limites à partir de sa dérivation (son intervalle de fluctuation), à chercher son extremum, à trouver ses asymptotes si elles existent, à tracer sa représentation graphique, puis à dresser le tableau de variation.
Le tableau de variation résume les informations importantes qui concernent les variations d'une fonction observée sur son ensemble de définition.

Le tableau indique les intervalles sur lesquelles la fonction est croissante ou décroissante, l'image des nombres pour lesquels la fonction admet une valeur maximale et minimale.
Ainsi voit-on, sur un tableau, deux lignes :
La première ligne, relative aux nombres-clés de l'ensemble de définition : les valeurs délimitant les intervalles de la fonction,
La seconde ligne, relative aux changements de variation de la fonction.
Logiquement, une flèche descendante indique que la fonction est décroissante.
A l'inverse, une flèche montante informe que la fonction est devenue croissante.
On renseigne parfois les valeurs pour lesquelles la fonction est nulle : grâce à cela, on repère les intervalles où la fonction admet des valeurs négatives ou positives.
Etudier les variations d'une fonction est donc un exercice de maths incontournable, qui revient très fréquemment dans les épreuves de mathématiques du baccalauréat, ainsi qu'à l'université dans les examens de licence (MASS, AES, etc.).
Cela servira évidemment aussi pour les cours de maths que les élèves peuvent prendre auprès de nos professeurs particuliers sur Superprof, ainsi que pour mieux réviser avec les annales bac.
Dériver une somme de fonctions avec constante
Pour savoir comment faire un tableau de variation, il faut préalablement pouvoir dériver la fonction à partir de l'équation donnée par l'énoncé.

Les dérivées des fonctions puissances, inverses et racines se calculent avec la formule suivante : si f(x) = xn+a, alors f '(x) = nxn-1+a.
Pour aider nos lecteurs, voici un très bon rappel du tableau des dérivées.
On s'explique :
Si f(x) = x²+1, alors on note sa dérivée f ' (x) = 2x +0, soit 2x.
Prenons l'exemple de f(x) = 10x²+5x +2 : on obtient f ' (x) = 10*2x2-1+5, soit f ' (x) = 20x +5 : la dérivée d'une constante est nulle.
On calcule chaque dérivée avec puissances de cette manière, donc si f(x) = x3, alors f ' (x) = 3x².
Prenons l'exemple de la fonction f(x) définie sur et donnée par f(x) = x3 + 3x2 -9x +6.
Sait-on déjà dériver la fonction, calculer le discriminant, dresser un tableau de signe d'une fonction dérivée, résoudre une inéquation, tracer des courbes sur un graphique sans confondre abscisse et ordonnée ?
Notre fonction f (x3 + 3x2 -9x +6) est une fonction polynôme formée par la somme de 3 termes de la forme "axn" (a et n étant des entiers naturels) et d'une constante (le nombre 6).
La dérivée de "axn" est de la forme "anxn-1", or la dérivée d'une constante est nulle.
La dérivée de f(x) est donc : f '(x) = 3x2 +6x -9.
Dériver une fonction avec un produit
Cela devient un peu plus compliqué lorsqu'une fonction se présente sous la forme d'un produit ou d'un quotient. Par exemple, f(x) = (2x+1) (x²-2).

Pour s'aider, voici une chaîne Youtube très pédagogique faite par un professeur de mathématiques :
En mathématiques, on note un produit de deux facteurs par u et v, soit ici, u = (2x+1) et v = (x²-2).
Pour dériver, on doit se souvenir des formules suivantes : (uv)' = u'v + uv'.
Il est recommandé d'écrire au brouillon chaque expression de u, u', v et v' :
- u = 2x+1,
- u' = 2,
- v = x²-2,
- v' = 2x.
L'on peut maintenant procéder à l'opération pour calculer la dérivée de f :
- f ' (x) = u'v + uv' = 2 (x²-2) + 2x (2x+1),
- f ' (x) = 2x² - 4 + 4x² + 2x,
- f ' (x) = 6x² + 2x - 4.
Factoriser si possible la dérivée de f
Le but de cette étape est de factoriser la dérivée de la fonction f(x) afin de l’exprimer sous la forme d’un produit ou d’un quotient d’expressions.
La factorisation est une étape clé qu'il ne faut pas oublier parce qu'elle facilite énormément l'étude du signe de f'(x).

Et oui la factorisation, c'est comme résoudre une énigme mathématiques en cours de maths.
Nous remarquons que dans notre fonction initiale (f(x) = x3 + 3x2 -9x +6), l'on peut prendre 3 en facteur ce qui donne : f'(x) = 3(x2 +2x -3).
x2 +2x -3 est un trinôme de second degré de la forme ax2 +bx +c avec a, b et c qui sont des nombres réels.
Pour factoriser ce trinôme il faut tout d'abord calculer le discriminant et trouver les racines x1 et x2.
Le discriminant est noté Δ.
Cela donne l'équation suivante : Δ = b2 -4ac, soit Δ = 22 -4×1×(-3) = 4 +12 = 16.
Le théorème du discriminant : si le discriminant est inférieur à 0, alors on admet qu'il n'y a pas de solution à l'équation.
- Si le résultat est nul, alors x = -b/2a.
- Si en revanche, Δ est positif, alors l'équation admet deux solutions distinctes telles que x1 = (-b + √Δ)/2a et x2 = ( -b - √Δ)/2a.
On peut alors calculer les racines via les deux formules suivantes :
- x1= (-2 - 4)/ 2 = -3,
- x2= (-2 + 4)/ 2 = 1.
Notons que si le discriminant est positif (et alors les deux racines existent), le trinôme peut être écrit sous la forme factorisée (x- x1) (x- x2), ce qui donne x2 +2x -3 = (x-(-3)) (x-1) = (x+3) (x-1).
La dérivée de la fonction s'écrit donc sous la forme factorisée suivante :
f'(x) = 3(x+3)(x-1)

Etudier le signe de f'(x) sur l’intervalle I
3 est un nombre positif donc le signe de la dérivée f'(x) est identique au signe de (x+3)(x-1).
On sait que si f'(x) est supérieure ou égale 0, alors la la fonction f est croissante sur I. A l'inverse, si f'(x) est inférieure ou égale à 0, alors f est décroissante sur I.
Pour connaître le signe de f', il suffit simplement de déterminer les valeurs de x pour lesquelles f'(x) s'annule, or on sait construire le tableau de signe d’une fonction de type ax + b.
- f '(x) = 3x2 +6x -9 = 3(x+3)(x-1),
- x+3 = 0 --> x=-3 et x-1=0 --> x=1.
Résolvons les inéquations suivantes :
- x + 3 > 0 => x > -3 donc le binôme x+3 est positif lorsque x est supérieur à -3, nul lorsque x est égal à -3 et négatif lorsque x est inférieur à -3.
- x - 1 > 0 => x > 1 donc le binôme x-1 est positif lorsque x est supérieur à 1, nul lorsque x est égal à 1 et négatif lorsque x est inférieur à 1.
Le tableau de signes de la dérivée f'(x) est présenté ci-dessous :
| x | - ∞ | -3 1 | +∞ |
| x + 3 | - 0 + + | ||
| x - 1 | - - 0 + | ||
| f'(x) | + 0 - 0 + |
f'(x) est donc croissante pour tout x défini sur l'intervalle ]-∞; -3], décroissante sur [-3 ; 1] et croissante sur [1 ; +∞[.
Notons que nous aurions pu déterminer le signe du trinôme x2 +2x -3 en utilisant une autre méthode.
En effet, quand le discriminant est positif, le trinôme ax²+bx+c prend le signe contraire de a dans l'intervalle compris entre les deux racines x1 et x2 et le même signe que a ailleurs.
Dresser le tableau de variation de f sur I

f étant dérivable sur I, pour toute valeur de x incluse dans I, on a :
- Si f'(x) > 0 pour tout x appartenant à I, alors f est strictement croissante sur I,
- Si f'(x) < 0 pour tout x appartenant à I, alors f est strictement décroissante sur I.
On en déduit alors le sens de variation de f, à partir du signe de la dérivée f'(x).
Si le signe de f'(x) est positif sur les intervalles ]-∞;-3] et sur [1;+∞[, alors la fonction f(x) est croissante sur ces deux intervalles.
Inversement, puisque le signe de f'(x) est négatif sut [-3;1], alors f(x) est décroissante sur ce même ensemble de définition.
Le tableau de variation de f est la représentation schématique des directions que prend la courbe représentative d’une fonction.
Pour s'entraîner avant le prochain cours de maths, placez les flèches sur le tableau ci-dessous.
Le tableau de variations de f est donné par :
| x | -∞ | -3 1 | +∞ |
| f(x) | 33 +∞
-∞ 1 |
On rappelle ici la fonction initiale : f(x) = x3 + 3x2 -9x +6.
En remplaçant la valeur de x par -3 et par 1, on obtient f(-3) = 33 et f(1) = 1.
Calculons maintenant les limites de la fonction.
On dit que tend vers l'infini (noté lorsque pour tout x suffisamment grand, est aussi grand que l’on veut.
On note alors : lim (x→+∞) f(x) = +∞.
D'après le tableau de variations de f, on constate que la fonction possède un maximum au point A (-3;33) et un minimum au point B (1;1).
Tracer la fonction sur son intervalle de définition
Pour tracer un graphique représentant cette fonction, il suffit de placer son minimum et son maximum sur le repère et de faire un petit tableau qui nous aide à poser quelque points particuliers :
| x | f (x) |
| -5 | 1 |
| -2 | 28 |
| -1 | 17 |
| 0 | 6 |
| 5 | 161 |
Et voici notre fameuse courbe :
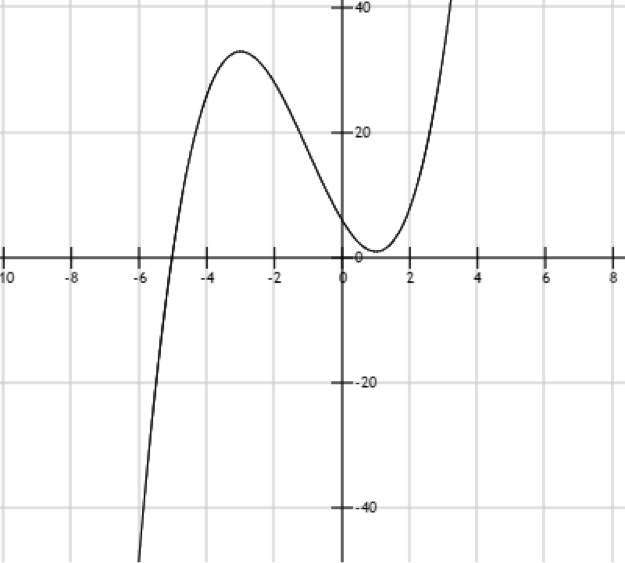
Les maths et l'art sont souvent liés, seulement une courbe mathématique, c'est tout sauf de l'art.
Faire bien attention à placer correctement les repères sur la courbe.
Liens pour s'entraîner aux épreuves de mathématiques :
- Annales bac,
- Tableau des dérivées.
Le tableau de variation d'une fonction sert à repérer facilement les asymptotes. Il s’acquiert généralement par l’étude du signe de la dérivée.

En cours de mathématiques, les élèves travaillent aussi des tableaux, avec leur prof de maths, qui ne représentent pas toute la fonction mais seulement une partie.
C'est le cas lorsqu'elle se répète à l’infini. Ces fonctions-là, sont dites périodiques.
Résoudre des problèmes en mathématiques est passionnant quand on sait les faire. Inversement, c'est un véritable calvaire lorsque l'on a pas eu le déclic.
Pour l'avoir - le déclic - il n'y a qu'une solution : il faut s'entraîner, s'entraîner encore, reprendre tous les exercices corrigés, et les refaire inlassablement, jusqu'à avoir une bonne compréhension des choses.
Personne n'est nul en maths !
Dresser un tableau de variation à partir d'une courbe
Il est possible d'utiliser la représentation graphique d'une fonction pour dresser son tableau de variation.
C'est la solution la plus facile car on ne va pas s'encombrer avec les calculs de dérivées, de limites et du discriminant.
- Commencez par distinguer les zones où la fonction devient croissante et décroissante.
- Ensuite, pour chacune des zones repérées, déterminez l'intervalle des abscisses : les extrémités inférieure et supérieure.
- Les reporter sur la première ligne du tableau.
- Faites ensuite correspondre dans la deuxième ligne une flèche montante pour chaque intervalle où la fonction est croissante, et une flèche descendante lorsqu'elle est décroissante.
- Repérez l'image de f sur la courbe pour chaque nombre de la première ligne du tableau.
- L'image de f correspond à l'ordonnée du point ayant ce nombre pour abscisse.
- Reporter ensuite l'image trouvée sous chaque nombre dans la deuxième ligne : on se réfère soit à l'origine d'une flèche, soit à sa pointe.

Ici, on voit que la fonction est croissante sur l'intervalle [-2;2], et constante sur les intervalles ]-∞;-2[ et ]2;+∞[.
Exercice pratique de variation d'une fonction
Pour bien saisir, on peut étudier ensemble une fonction.
Soit f(x) = x3-12x+1, définie sur R.
On va d'abord calculer la dérivée, chercher le signe de la dérivée et donner les variations de la fonction sous la forme d'un tableau à deux lignes.
La dérivée f'(x) = 3x²-12, soit 3(x²-4) = 3(x-2)(x+2).
Comme il s'agit d'un produit, on sait que la dérivée s'annule pour x=-2 ou pour x=2.
Un tableau de signe peut indiquer que la dérivée est positive sur ]-∞;-2], négative sur ]-2;2[ et positive sur [2;+∞[.
On va ensuite calculer les valeurs de la fonction pour les reporter ensuite dans le tableau de signes.
- Pour f(-2) : f(-2) =(-2)3-12x(-2)+1 = -8+25 = 17.
- Pour f(2) : f(2) = 8-24 + 1 = -15.
On dresse ensuite le tableau de variation, en prenant soin de reporter les valeurs déterminées.
Grâce au tableau et à la représentation graphique, on peut déduire que l'équation f(x)=0 aura trois solutions dans R :
- Une solution sur l'intervalle ]-∞;-2], la fonction admettant des valeurs de signes négatif puis positif,
- Une solution sur l'intervalle ]-2;2] : la fonction passe par 0 car elle admet des valeurs positives, puis négatives,
- Une solution sur ]2;+∞[ car la fonction devient négative puis positive : elle passe donc pas 0.
Vous avez tout suivi ?

Voici maintenant pour vous entraîner... Une interrogation surprise !
- Soit la fonction f(x) = 2x3+5x2-4x + 1, définie sur [-100 ; 100],
- Dériver f(x),
- Étudier le sens de variation de la fonction dérivée,
- f(x) est-elle croissante sur [-100 ; -50] ?
- Dresser un tableau de variation de la fonction,
- Tracer la représentation graphique de la fonction f.
Maîtriser le tableau de variation d'une fonction permet de vous faire gagner des points lors du contrôle continu : ce n'est donc pas un chapitre du programme de maths à négliger !
Et si vous preniez des cours particuliers pour étudier d'autres aspects des maths ? Tangente, axe des abscisses, fonction définie ou cosinus : autant de thèmes à aborder pendant un cours de maths en ligne !
















Je l’aimais beaucoup ce cours
J’ai beaucoup apprécié ce cours !
Je vraiment aimé ce cours merci beaucoup et j’aimerais davantage sur ce DM svp comment procéder à cette fonction de dérivée ci dessous ?
Soit la fonction f(x) = 2×3+5×2-4x + 1, définie sur [-100 ; 100],
Dériver f(x),
Étudier le sens de variation de la fonction dérivée,
f(x) est-elle croissante sur [-100 ; -50] ?
Dresser un tableau de variation de la fonction,
Tracer la représentation graphique de la fonction f.
Merci bien le cours est bien complet. Sinon, un cours des valeurs approchées ?
Quelle est la méthode pour dresser un tableau de variation d’une fonction exponentielle ? Faut-il déterminer les racines ou bien les limites ?
cela dépend de ton intervalle mais ce sont souvent les limites qui sont demandées
Bonsoir,
J’ai pu me remémorer les sens de variation d’une fonction que j’avais oubliés.
Merci.
Le cours était parfait
Bonjours comment faire pour dresser le tableau de variation lorsque la dérivée est f'(x)= -2x+10-8/x ? La fonction de départ est f(x)= -2x+10x-9-8ln(x)
Bonjour Céline,
Il faut commencer par étudier le signe de f'(x) en cherchant à savoir quand f'(x) s’annule. Une fois cette information trouvée, il vous sera plus simple de dresser le tableau de variation et de chercher ses limites.
Si vous avez besoin d’aide, n’hésitez pas à faire appel à un professeur particulier sur Superprof. Une application peut également vous aider dans ce cas : SnapSchool. Il vous suffit de poster votre problème pour trouver de l’aide auprès d’autres élèves.
Bon courage et bonne réussite !
Bonjours pouvez vous m’aider pour établir un tableau de variations ?
Bonjour,
Vous pouvez demander de l’aide à l’un de nos professeurs en mathématiques. Pour cela, regardez les profils présents dans votre région et contactez-les après inscription. Si vous êtes mineur, il faudra donc voir cela avec vos parents.
Vous pouvez également demander de l’aide à votre professeur de mathématiques.
Bien à vous
cours interressant
Comment établir le tableau de variation ??
cours interressant wesh
cool
je suis vraiment content de ce contenu
bonjour, comment dresser le tableau avec une dérivée égale à g'(x)= 3x(2+x)
merci :)
Bonjour,
Même conseil que pour Céline: commencez par étudier le signe de g'(x) en cherchant à savoir quand g'(x) s’annule.Vous pourrez ensuite trouver le tableau des variations et les limites.
L’aide d’un professeur particulier pourra éventuellement vous être utile pour l’aide aux devoirs. Faites également un petit tour sur l’application « SnapSchool » pour trouver l’aide de vos camarades.
Bonne continuation
Bonjour, pourriez vous me dire comment dresser le tableau de variations de la fonction suivante svp ? :
f(x) = x-1/x avec un intervalle I = tous les réels sauf 0
Bonjour,
L’article ci-dessus vous donne toutes les clefs et les étapes pour dresser le tableau de variations de votre fonction.
Bon courage
Salut pouvez vous m’aider ?
Bonjour,
Merci pour votre commentaire, en quoi pourrions-nous vous aider ?
Bien à vous
merci beaucoup pour ces cours cest tres interessant pour les eleves merci pour vos efforts
Grâce à ce cours, j’ai pu approfondir l la notion de tableau de variation.
Vraiment j’aime beaucoup la façon d’expliquer et j’ai compris après votre explication
Bonjour,
Merci pour votre commentaire.
Bien à vous
Cela ne pas aider pour mon devoir de math mais merci quand mème.
Moi mes problèmes sont: tableau de signe et variation et étude de la variation d’une.